
Ergodic Fluctuations Between Stochastic Simulation Realizations#
Michael J. Pyrcz, Professor, The University of Texas at Austin
Twitter | GitHub | Website | GoogleScholar | Book | YouTube | Applied Geostats in Python e-book | LinkedIn
Chapter of e-book “Applied Geostatistics in Python: a Hands-on Guide with GeostatsPy”.
Cite this e-Book as:
Pyrcz, M.J., 2024, Applied Geostatistics in Python: a Hands-on Guide with GeostatsPy [e-book]. Zenodo. doi:10.5281/zenodo.15169133
The workflows in this book and more are available here:
Cite the GeostatsPyDemos GitHub Repository as:
Pyrcz, M.J., 2024, GeostatsPyDemos: GeostatsPy Python Package for Spatial Data Analytics and Geostatistics Demonstration Workflows Repository (0.0.1) [Software]. Zenodo. doi:10.5281/zenodo.12667036. GitHub Repository: GeostatsGuy/GeostatsPyDemos
By Michael J. Pyrcz
© Copyright 2024.
This chapter is a tutorial for / demonstration of Ergodic Fluctuations Between Stochastic Simulation Realizations.
this is the fluctuations in the reproduction of input statistics over multiple simulation realizations.
YouTube Lecture: check out my lectures:
For your convenience here’s a summary of salient points.
Estimation vs. Simulation#
Let’s start by comparing spatial estimation and simulation,
Estimation:
honors local data
locally accurate, primary goal of estimation is 1 estimate!
too smooth, appropriate for visualizing trends
too smooth, inappropriate for flow simulation
one model, no assessment of global uncertainty
Let’s visualize a population, sample and estimation model. Note the estimation model is too smooth, too much spatial continuity and too little variance.
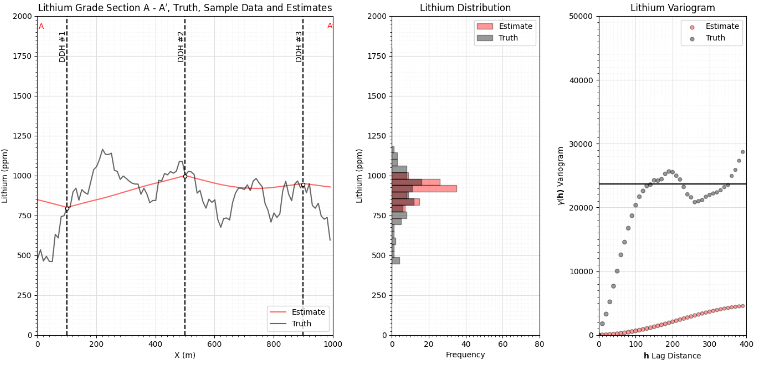
Simulation:
honors local data
sacrifices local accuracy, reproduces histogram
honors spatial variability, appropriate for flow simulation
alternative realizations, change random number seed
many models (realizations), assessment of global uncertainty
Now let’s visualize a population, sample and simulation model. Note the simulated realizations are locally less accurate, but are not too smooth, the spatial continuity and variance are correct.
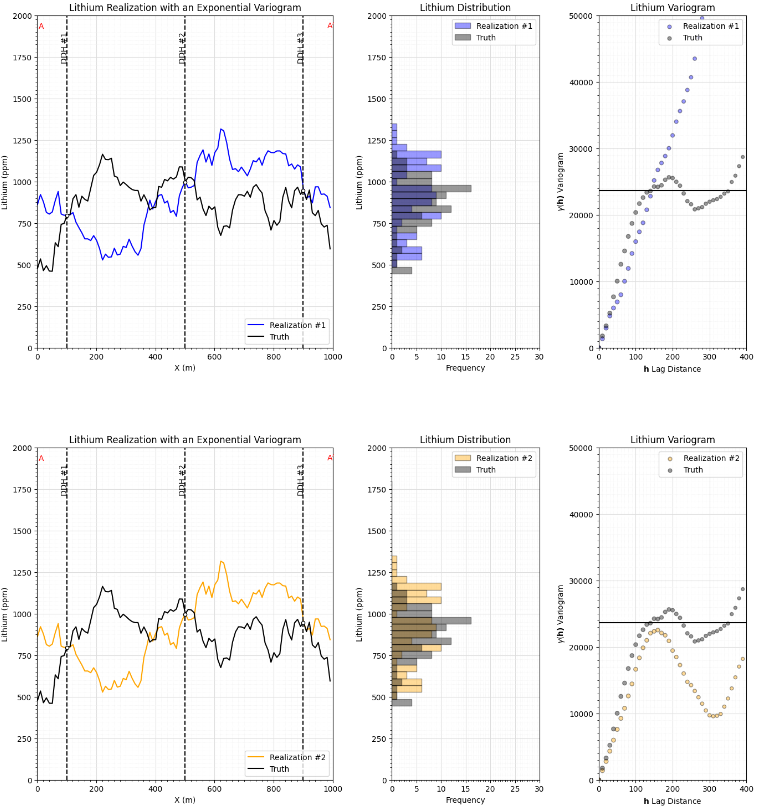
Note with estimation we calculate one model, and with simulation we calculate many realizations to represent uncertainty,
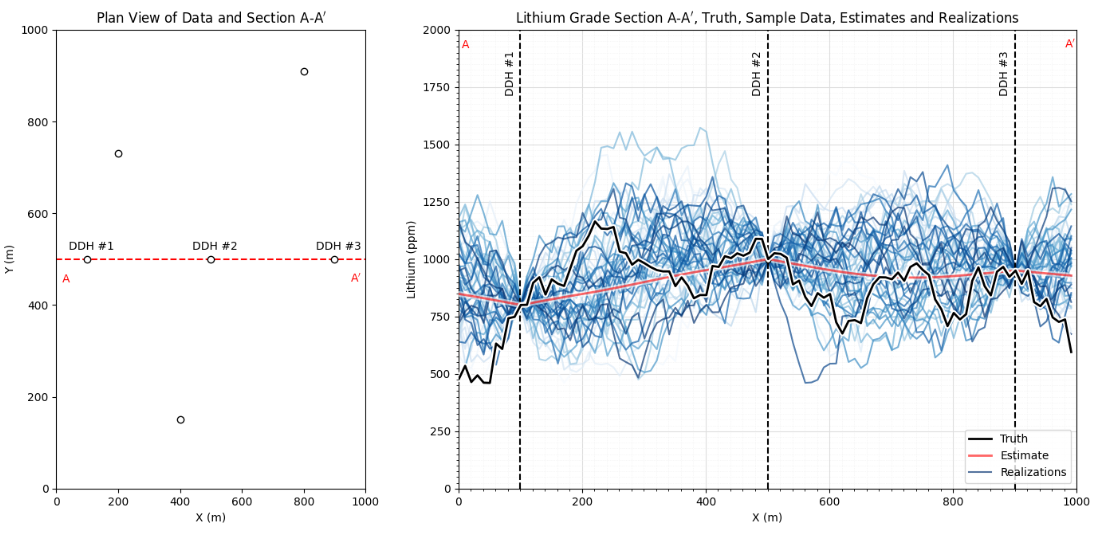
Ergodic Fluctuations#
Simulation honors global statistics in expected value over multiple realizations:
Expect some statistical fluctuation in the input statistics
These are a function of the ratio of spatial continuity to the size of the model.
If model is large relative to spatial continuity range then fluctuations should minimal
If model is small relative to spatial continuity range then fluctuations may be extreme
In the case of the global mean we can calculate the variance in the means over multiple realizations prior to actually calculating the simulation realizations.
the variance in the mean over realizations is the dispersion variance of the volume of interest in an infinite domain, to learn more about dispersion variance check out my lecture Dispersion Variance and linked demonstrations.
In this workflow we run multiple simulation realizations, calculate the statistics and observe these fluctuations.
Load the Required Libraries#
The following code loads the required libraries.
import geostatspy.GSLIB as GSLIB # GSLIB utilities, visualization and wrapper
import geostatspy.geostats as geostats # GSLIB methods convert to Python
import geostatspy
print('GeostatsPy version: ' + str(geostatspy.__version__))
GeostatsPy version: 0.0.71
We will also need some standard packages. These should have been installed with Anaconda 3.
import os # set working directory, run executables
from tqdm import tqdm # suppress the status bar
from functools import partialmethod
tqdm.__init__ = partialmethod(tqdm.__init__, disable=True)
ignore_warnings = True # ignore warnings?
import numpy as np # ndarrays for gridded data
import pandas as pd # DataFrames for tabular data
import os # set working directory, run executables
import matplotlib.pyplot as plt # for plotting
from matplotlib.ticker import (MultipleLocator, AutoMinorLocator) # control of axes ticks
from matplotlib import gridspec # custom subplots
plt.rc('axes', axisbelow=True) # plot all grids below the plot elements
if ignore_warnings == True:
import warnings
warnings.filterwarnings('ignore')
from IPython.utils import io # mute output from simulation
Simulation Parameters, Data with Reference Distribution#
We need a full reference distribution for the feature of interest, but for unconditional simulated realizations.
we accomplish this with a set of data samples outside the range of spatial correlation from the AOI.
this is used by the sequential Gaussian simulation program to support the distribution backtransformation from Gaussian space.
while the data will inform the distribution transformation, they are outside the range of spatial continuity and will not locally condition the model
nx = 100; ny = 1; xsiz = 10.0; ysiz = 10.0; xmn = 5.0; ymn = 5.0; nxdis = 1; nydis = 1 # grid specification
ndmin = 0; ndmax = 20; radius = 2000; skmean = 0; tmin = -99999; tmax = 99999; nreal = 10 # simulation parameters
df = pd.DataFrame(np.vstack([np.full(1000,-9999),np.random.normal(size=1000), # reference distribution outside VOI
np.random.normal(loc=1000,scale=200,size=1000)]).T, columns= ['X','Y','Lithium'])
df.loc[0,'X'] = 105; df.loc[0,'Y'] = 5.0; df.loc[0,'Lithium'] = 800 # add 3 data in VOI for visualization of conditioning
df.loc[1,'X'] = 505; df.loc[1,'Y'] = 5.0; df.loc[1,'Lithium'] = 1000
df.loc[2,'X'] = 905; df.loc[2,'Y'] = 5.0; df.loc[2,'Lithium'] = 950
df.head()
| X | Y | Lithium | |
|---|---|---|---|
| 0 | 105.0 | 5.000000 | 800.000000 |
| 1 | 505.0 | 5.000000 | 1000.000000 |
| 2 | 905.0 | 5.000000 | 950.000000 |
| 3 | -9999.0 | 1.116678 | 1017.717572 |
| 4 | -9999.0 | 0.104503 | 1054.145254 |
Make Truth Model#
For visualization, simulate a consistent truth model.
we use the same reference distribution and variogram model for truth and realizations, assuming perfect / no error inference
vario_truth = GSLIB.make_variogram(nug=0.0,nst=1,it1=1,cc1=1.0,azi1=90.0,hmaj1=100,hmin1=5) # truth variogram
fig = plt.figure()
grid_spec = gridspec.GridSpec(ncols = 2,nrows=1,width_ratios=[1, 2])
ax0 = fig.add_subplot(grid_spec[0])
ax0.scatter([100,500,900,400,200,800],[500,500,500,150,730,910],color='white',edgecolor='black',zorder=10) # data for viz
plt.plot([0,1000],[500,500],ls='--',color='red',zorder=1)
plt.annotate(r'DDH #1',(40,520)); plt.annotate(r'DDH #2',(440,520)) # plot 3 conditioning data
plt.annotate(r'DDH #3',(840,520))
plt.annotate(r'A',(20,450),color='red'); plt.annotate(r'A$^\prime$',(950,450),color='red')
plt.xlim([0,1000]); plt.ylim([0,1000]); plt.xlabel('X (m)'); plt.ylabel('Y (m)'); plt.title('Plan View of Data and Section A-A$^\prime$')
ax1 = fig.add_subplot(grid_spec[1]) # cross section
with io.capture_output() as captured: # mute simulation output
truth = geostats.sgsim(df,'X','Y','Lithium',wcol=-1,scol=-1,tmin=tmin,tmax=tmax,itrans=1,ismooth=0,dftrans=0,tcol=0,
twtcol=0,zmin=0.0,zmax=2000.0,ltail=1,ltpar=0.0,utail=1,utpar=2000,nsim=1,
nx=nx,xmn=xmn,xsiz=xsiz,ny=ny,ymn=ymn,ysiz=ysiz,seed=72067,
ndmin=ndmin,ndmax=ndmax,nodmax=10,mults=0,nmult=2,noct=-1,
ktype=0,colocorr=0.0,sec_map=0,vario=vario_truth)[0][0]
ax1.plot(np.arange(1,(nx*xsiz),xsiz),truth,color='black',label='Truth',zorder=1)
plt.annotate(r'DDH #1',(80,1720),rotation = 90); plt.annotate(r'DDH #2',(480,1720),rotation = 90)
plt.annotate(r'DDH #3',(880,1720),rotation = 90)
plt.annotate(r'A',(5,1920),color='red'); plt.annotate(r'A$^\prime$',(980,1920),color='red')
plt.scatter(500,995,s=20,color='white',edgecolor='black',zorder=10); plt.scatter(100,795,s=20,color='white',edgecolor='black',zorder=10)
plt.scatter(900,945,s=20,color='white',edgecolor='black',zorder=10)
plt.plot([100,100],[0,2000],color='black',ls='--'); plt.plot([900,900],[0,2000],color='black',ls='--')
plt.plot([500,500],[0,2000],color='black',ls='--')
plt.legend(loc='lower right')
plt.ylim([0,2000]); plt.xlim([0,1000])
gca = plt.gca()
gca.xaxis.set_minor_locator(AutoMinorLocator(10))
gca.yaxis.set_minor_locator(AutoMinorLocator(10))
gca.grid(which='major', color='#DDDDDD', linewidth=0.8); gca.grid(which='minor',color='#EEEEEE', linestyle=':', linewidth=0.5)
plt.xlabel('X (m)'); plt.ylabel('Lithium (ppm)'); plt.title('Lithium Grade Section A - A$^\prime$ and 3 Sample Data')
plt.subplots_adjust(left=0.0, bottom=0.0, right=2.0, top=1.0, wspace=0.2, hspace=0.2); plt.show()
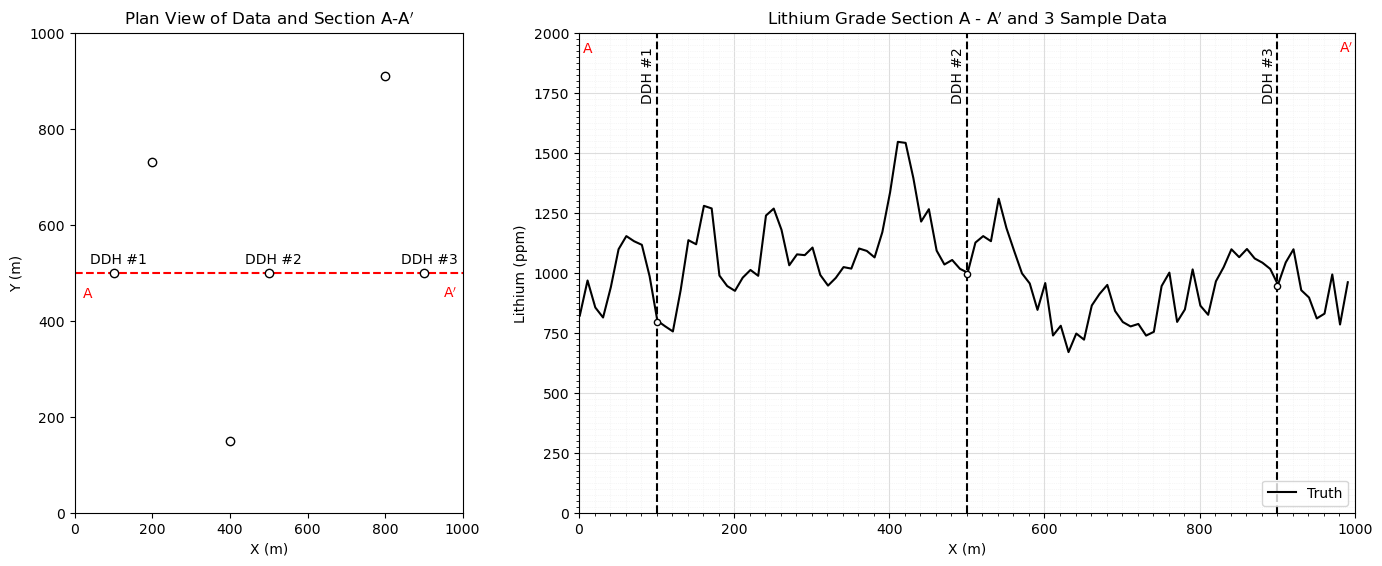
Many Simulated Realizations#
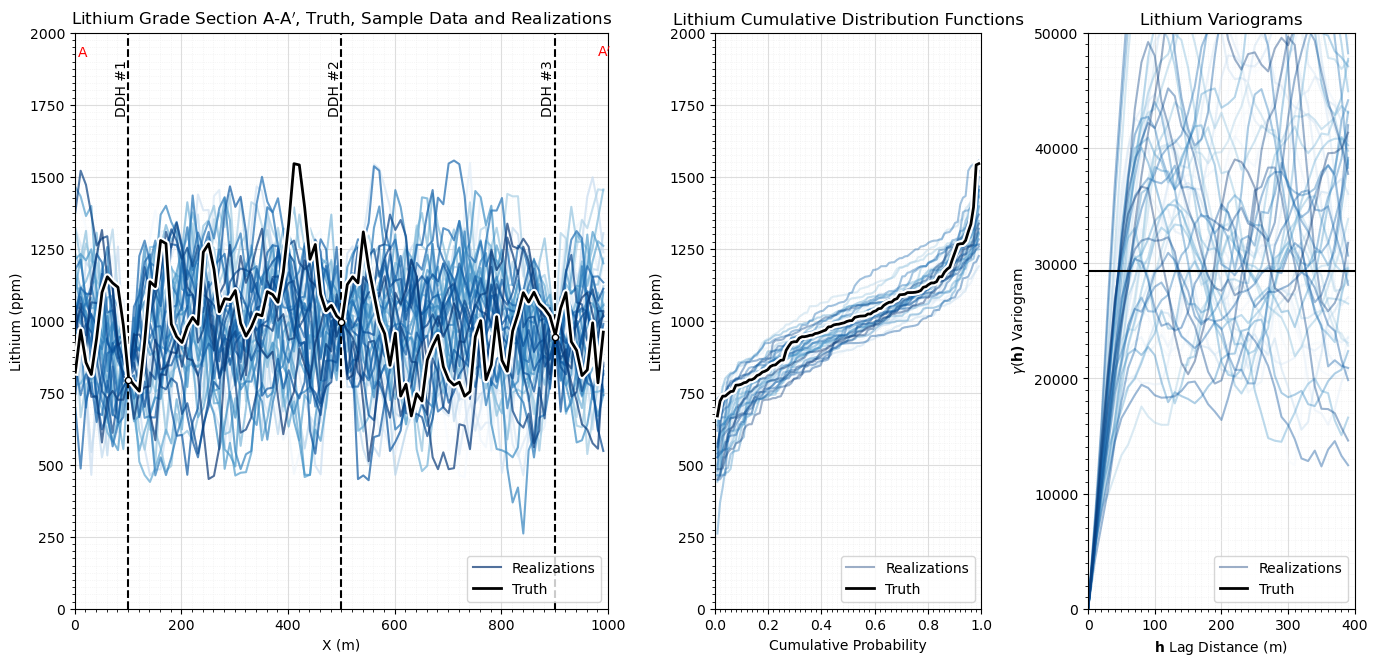
Now let’s make many realizations and compare their statistics, cumulative distribution functions and variograms, to the original data statistics.
we will see fluctuations in the CDFs and experimental variograms
these fluctuations increase as the ratio of variogram range / model extent increases.
nreal = 50 # number of realizations
fig = plt.figure()
grid_spec = gridspec.GridSpec(ncols = 3,nrows=1,width_ratios=[2, 1, 1])
ax0 = fig.add_subplot(grid_spec[0])
with io.capture_output() as captured:
sim = geostats.sgsim(df,'X','Y','Lithium',wcol=-1,scol=-1,tmin=tmin,tmax=tmax,itrans=1,ismooth=0,dftrans=0,tcol=0,
twtcol=0,zmin=0.0,zmax=2000.0,ltail=1,ltpar=0.0,utail=1,utpar=2000,nsim=nreal,
nx=nx,xmn=xmn,xsiz=xsiz,ny=ny,ymn=ymn,ysiz=ysiz,seed=83090,
ndmin=ndmin,ndmax=ndmax,nodmax=10,mults=0,nmult=2,noct=-1,
ktype=0,colocorr=0.0,sec_map=0,vario=vario_truth).reshape((nreal,nx)) # nd_array[nreal,nx] of realizations
for i in range(0, nreal):
if i == nreal - 1:
ax0.plot(np.arange(1,(nx*xsiz),xsiz),sim[i],color=plt.cm.Blues(i/nreal),alpha=0.7,zorder=1,label='Realizations')
else:
ax0.plot(np.arange(1,(nx*xsiz),xsiz),sim[i],color=plt.cm.Blues(i/nreal),alpha=0.7,zorder=1)
ax0.plot(np.arange(1,(nx*xsiz),xsiz),truth,color='black',label='Truth',lw=2,zorder=10)
ax0.plot(np.arange(1,(nx*xsiz),xsiz),truth,color='white',lw=5,zorder=5)
plt.annotate(r'DDH #1',(75,1720),rotation = 90); plt.annotate(r'DDH #2',(475,1720),rotation = 90)
plt.annotate(r'DDH #3',(875,1720),rotation = 90)
plt.annotate(r'A',(5,1920),color='red'); plt.annotate(r'A$^\prime$',(980,1920),color='red')
plt.scatter(500,995,s=20,color='white',edgecolor='black',zorder=10); plt.scatter(100,795,s=20,color='white',edgecolor='black',zorder=10)
plt.scatter(900,945,s=20,color='white',edgecolor='black',zorder=10)
plt.plot([100,100],[0,2000],color='black',ls='--'); plt.plot([900,900],[0,2000],color='black',ls='--')
plt.plot([500,500],[0,2000],color='black',ls='--')
plt.ylim([0,2000]); plt.xlim([0,1000])
gca = plt.gca()
gca.xaxis.set_minor_locator(AutoMinorLocator(10))
gca.yaxis.set_minor_locator(AutoMinorLocator(10))
gca.grid(which='major', color='#DDDDDD', linewidth=0.8)
gca.grid(which='minor',color='#EEEEEE', linestyle=':', linewidth=0.5)
plt.xlabel('X (m)'); plt.ylabel('Lithium (ppm)'); plt.title('Lithium Grade Section A-A$^\prime$, Truth, Sample Data and Realizations')
plt.legend(loc='lower right')
ax1 = fig.add_subplot(grid_spec[1]) # visualize the CDFs
for i in range(0, nreal):
sim_sort = np.sort(sim[i])
p = ((np.arange(len(sim[i])))+1)/(len(sim[i]) + 1) # CDF unknown lower and upper tail assumption
if i == nreal-1:
plt.plot(p,sim_sort,c = plt.cm.Blues(i/nreal),alpha = 0.4,zorder=1,label='Realizations')
else:
plt.plot(p,sim_sort,c = plt.cm.Blues(i/nreal),alpha = 0.4,zorder=1)
truth_sort = np.sort(truth)
p = ((np.arange(len(truth)))+1)/(len(truth) + 1) # CDF unknown lower and upper tail assumption
plt.plot(p,truth_sort,c = 'white',lw=5,zorder=5)
plt.plot(p,truth_sort,c = 'black',lw=2,zorder=10,label='Truth')
plt.ylabel('Lithium (ppm)'); plt.xlabel('Cumulative Probability'); plt.grid();
plt.title('Lithium Cumulative Distribution Functions')
plt.xlim([0,1]); plt.ylim([0,2000])
gca= plt.gca()
gca.xaxis.set_minor_locator(AutoMinorLocator(10))
gca.yaxis.set_minor_locator(AutoMinorLocator(10))
gca.grid(which='major', color='#DDDDDD', linewidth=0.8)
gca.grid(which='minor',color='#EEEEEE', linestyle=':', linewidth=0.5)
plt.legend(loc='lower right')
ax2 = fig.add_subplot(grid_spec[2]) # visualize experimental variograms
truth_series = pd.Series(truth[0]); gamma_truth = []; num_pairs_all = []
for ilag in range(0,40):
num_pairs_all.append(float(len((truth_series - truth_series.shift(ilag)).dropna())))
gamma_truth.append(np.average(np.square((truth_series - truth_series.shift(ilag)).dropna()))*0.5)
lithium_var = np.var(truth)
for i in range(0, nreal):
sim_series = pd.Series(sim[i])
gamma_sim = []
for ilag in range(0,40):
num_pairs_all.append(float(len((truth_series - truth_series.shift(ilag)).dropna())))
gamma_sim.append(np.average(np.square((sim_series - sim_series.shift(ilag)).dropna()))*0.5)
if i == nreal-1:
scatter = ax2.plot(np.arange(0,40)*xsiz,gamma_sim,color=plt.cm.Blues(i/nreal),alpha=0.4,label='Realizations')
else:
scatter = ax2.plot(np.arange(0,40)*xsiz,gamma_sim,color=plt.cm.Blues(i/nreal),alpha=0.4)
plt.plot(np.arange(0,40)*xsiz,gamma_truth,c = 'white',lw=5,zorder=5)
plt.plot(np.arange(0,40)*xsiz,gamma_truth,c = 'black',lw=2,zorder=10,label='Truth')
plt.plot([0,400],[lithium_var,lithium_var],color='black')
plt.xlim([0,400]); plt.ylim([0,50000]); plt.title('Lithium Variograms')
plt.xlabel(r'$\bf{h}$ Lag Distance (m)'); plt.ylabel(r'$\gamma(\bf{h})$ Variogram')
gca = plt.gca()
gca.xaxis.set_minor_locator(AutoMinorLocator(10))
gca.yaxis.set_minor_locator(AutoMinorLocator(10))
gca.grid(which='major', color='#DDDDDD', linewidth=0.8)
gca.grid(which='minor',color='#EEEEEE', linestyle=':', linewidth=0.5)
plt.legend(loc='lower right')
plt.subplots_adjust(left=0.0, bottom=0.0, right=2.0, top=1.2, wspace=0.3, hspace=0.2); plt.show()
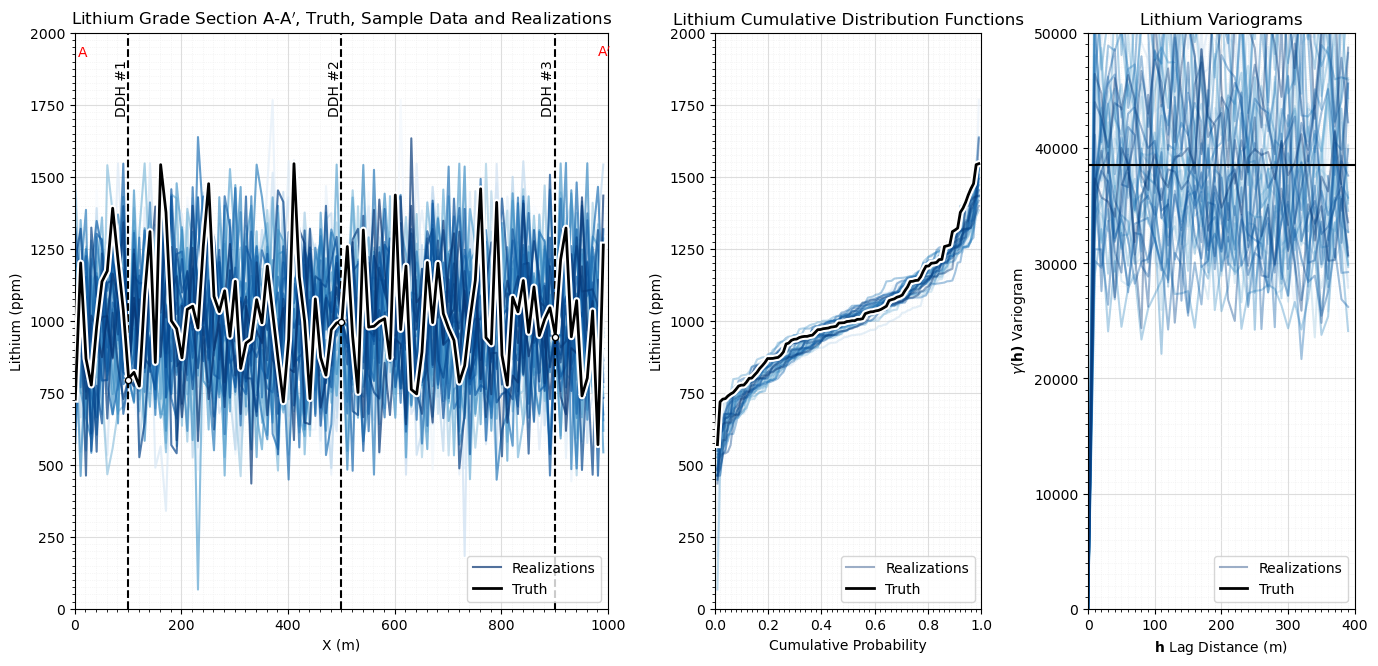
Short Range Continuity Case#
Let’s repeat the above for a short range continuity case.
nreal = 50; vrange = 10 # number of realizations and variogram range
vario1 = GSLIB.make_variogram(nug=0.0,nst=1,it1=1,cc1=1.0,azi1=90.0,hmaj1=vrange,hmin1=5)
with io.capture_output() as captured:
truth = geostats.sgsim(df,'X','Y','Lithium',wcol=-1,scol=-1,tmin=tmin,tmax=tmax,itrans=1,ismooth=0,dftrans=0,tcol=0,
twtcol=0,zmin=0.0,zmax=2000.0,ltail=1,ltpar=0.0,utail=1,utpar=2000,nsim=1,
nx=nx,xmn=xmn,xsiz=xsiz,ny=ny,ymn=ymn,ysiz=ysiz,seed=72067,
ndmin=ndmin,ndmax=ndmax,nodmax=10,mults=0,nmult=2,noct=-1,
ktype=0,colocorr=0.0,sec_map=0,vario=vario1)[0][0]
fig = plt.figure()
grid_spec = gridspec.GridSpec(ncols = 3,nrows=1,width_ratios=[2, 1, 1])
ax0 = fig.add_subplot(grid_spec[0]) # visualize the truth and realizations
with io.capture_output() as captured:
sim = geostats.sgsim(df,'X','Y','Lithium',wcol=-1,scol=-1,tmin=tmin,tmax=tmax,itrans=1,ismooth=0,dftrans=0,tcol=0,
twtcol=0,zmin=0.0,zmax=2000.0,ltail=1,ltpar=0.0,utail=1,utpar=2000,nsim=nreal,
nx=nx,xmn=xmn,xsiz=xsiz,ny=ny,ymn=ymn,ysiz=ysiz,seed=83090+i,
ndmin=ndmin,ndmax=ndmax,nodmax=10,mults=0,nmult=2,noct=-1,
ktype=0,colocorr=0.0,sec_map=0,vario=vario1).reshape((nreal,nx))
for i in range(0, nreal):
if i == nreal - 1:
ax0.plot(np.arange(1,(nx*xsiz),xsiz),sim[i],color=plt.cm.Blues(i/nreal),alpha=0.7,zorder=1,label='Realizations')
else:
ax0.plot(np.arange(1,(nx*xsiz),xsiz),sim[i],color=plt.cm.Blues(i/nreal),alpha=0.7,zorder=1)
ax0.plot(np.arange(1,(nx*xsiz),xsiz),truth,color='black',label='Truth',lw=2,zorder=10)
ax0.plot(np.arange(1,(nx*xsiz),xsiz),truth,color='white',lw=5,zorder=5)
plt.annotate(r'DDH #1',(75,1720),rotation = 90); plt.annotate(r'DDH #2',(475,1720),rotation = 90)
plt.annotate(r'DDH #3',(875,1720),rotation = 90)
plt.annotate(r'A',(5,1920),color='red'); plt.annotate(r'A$^\prime$',(980,1920),color='red')
plt.scatter(500,995,s=20,color='white',edgecolor='black',zorder=10); plt.scatter(100,795,s=20,color='white',edgecolor='black',zorder=10)
plt.scatter(900,945,s=20,color='white',edgecolor='black',zorder=10)
plt.plot([100,100],[0,2000],color='black',ls='--'); plt.plot([900,900],[0,2000],color='black',ls='--')
plt.plot([500,500],[0,2000],color='black',ls='--')
plt.ylim([0,2000]); plt.xlim([0,1000])
gca = plt.gca()
gca.xaxis.set_minor_locator(AutoMinorLocator(10))
gca.yaxis.set_minor_locator(AutoMinorLocator(10))
gca.grid(which='major', color='#DDDDDD', linewidth=0.8)
gca.grid(which='minor',color='#EEEEEE', linestyle=':', linewidth=0.5)
plt.xlabel('X (m)'); plt.ylabel('Lithium (ppm)'); plt.title('Lithium Grade Section A-A$^\prime$, Truth, Sample Data and Realizations')
plt.legend(loc='lower right')
ax1 = fig.add_subplot(grid_spec[1]) # visualize the CDFs
for i in range(0, nreal):
sim_sort = np.sort(sim[i])
p = ((np.arange(len(sim[i])))+1)/(len(sim[i]) + 1) # CDF unknown lower and upper tail assumption
if i == nreal-1:
plt.plot(p,sim_sort,c = plt.cm.Blues(i/nreal),alpha = 0.4,zorder=1,label='Realizations')
else:
plt.plot(p,sim_sort,c = plt.cm.Blues(i/nreal),alpha = 0.4,zorder=1)
truth_sort = np.sort(truth)
p = ((np.arange(len(truth)))+1)/(len(truth) + 1) # CDF unknown lower and upper tail assumption
plt.plot(p,truth_sort,c = 'white',lw=5,zorder=5)
plt.plot(p,truth_sort,c = 'black',lw=2,zorder=10,label='Truth')
plt.ylabel('Lithium (ppm)'); plt.xlabel('Cumulative Probability'); plt.grid();
plt.title('Lithium Cumulative Distribution Functions')
plt.xlim([0,1]); plt.ylim([0,2000])
gca= plt.gca()
gca.xaxis.set_minor_locator(AutoMinorLocator(10))
gca.yaxis.set_minor_locator(AutoMinorLocator(10))
gca.grid(which='major', color='#DDDDDD', linewidth=0.8)
gca.grid(which='minor',color='#EEEEEE', linestyle=':', linewidth=0.5)
plt.legend(loc='lower right')
ax2 = fig.add_subplot(grid_spec[2]) # visualize experimental variograms
truth_series = pd.Series(truth[0]); gamma_truth = []; num_pairs_all = []
for ilag in range(0,40):
num_pairs_all.append(float(len((truth_series - truth_series.shift(ilag)).dropna())))
gamma_truth.append(np.average(np.square((truth_series - truth_series.shift(ilag)).dropna()))*0.5)
lithium_var = np.var(truth)
for i in range(0, nreal):
sim_series = pd.Series(sim[i])
gamma_sim = []
for ilag in range(0,40):
num_pairs_all.append(float(len((truth_series - truth_series.shift(ilag)).dropna())))
gamma_sim.append(np.average(np.square((sim_series - sim_series.shift(ilag)).dropna()))*0.5)
if i == nreal-1:
scatter = ax2.plot(np.arange(0,40)*xsiz,gamma_sim,color=plt.cm.Blues(i/nreal),alpha=0.4,label='Realizations')
else:
scatter = ax2.plot(np.arange(0,40)*xsiz,gamma_sim,color=plt.cm.Blues(i/nreal),alpha=0.4)
plt.plot(np.arange(0,40)*xsiz,gamma_truth,c = 'white',lw=5,zorder=5)
plt.plot(np.arange(0,40)*xsiz,gamma_truth,c = 'black',lw=2,zorder=10,label='Truth')
plt.plot([0,400],[lithium_var,lithium_var],color='black')
plt.xlim([0,400]); plt.ylim([0,50000]); plt.title('Lithium Variograms')
plt.xlabel(r'$\bf{h}$ Lag Distance (m)'); plt.ylabel(r'$\gamma(\bf{h})$ Variogram')
gca = plt.gca()
gca.xaxis.set_minor_locator(AutoMinorLocator(10))
gca.yaxis.set_minor_locator(AutoMinorLocator(10))
gca.grid(which='major', color='#DDDDDD', linewidth=0.8)
gca.grid(which='minor',color='#EEEEEE', linestyle=':', linewidth=0.5)
plt.legend(loc='lower right')
plt.subplots_adjust(left=0.0, bottom=0.0, right=2.0, top=1.2, wspace=0.3, hspace=0.2); plt.show()
Want to Work Together?#
I hope this content is helpful to those that want to learn more about subsurface modeling, data analytics and machine learning. Students and working professionals are welcome to participate.
Want to invite me to visit your company for training, mentoring, project review, workflow design and / or consulting? I’d be happy to drop by and work with you!
Interested in partnering, supporting my graduate student research or my Subsurface Data Analytics and Machine Learning consortium (co-PI is Professor John Foster)? My research combines data analytics, stochastic modeling and machine learning theory with practice to develop novel methods and workflows to add value. We are solving challenging subsurface problems!
I can be reached at mpyrcz@austin.utexas.edu.
I’m always happy to discuss,
Michael
Michael Pyrcz, Ph.D., P.Eng. Professor, Cockrell School of Engineering and The Jackson School of Geosciences, The University of Texas at Austin
More Resources Available at: Twitter | GitHub | Website | GoogleScholar | Geostatistics Book | YouTube | Applied Geostats in Python e-book | Applied Machine Learning in Python e-book | LinkedIn


Comments#
This was a basic demonstration ergodic fluctuations for a simulated lithium grade model. Much more can be done, I have other demonstrations for modeling workflows with GeostatsPy in the GitHub repository GeostatsPy_Demos.
I hope this is helpful,
Michael