Cosimulation#
Michael Pyrcz, Professor, The University of Texas at Austin#
Twitter | GitHub | Website | GoogleScholar | Book | YouTube | LinkedIn#
This is a tutorial for / demonstration of Cosimulation by Sequential Gaussian Simulation with Colocated Cokriging with a 2D map example.
this is the fluctuations in the reproduction of input statistics over multiple simulation realizations.
YouTube Lecture: check out my lectures on:
For your convenience here’s a summary of salient points. First, let’s explain the concept of spatial simulation (1 feature).
Sequential Gaussian Simulation#
With sequential Gaussian simulation we build on kriging by:
adding a random residual with the missing variance
sequentially adding the simulated values as data to correct the covariance between the simulated values
The resulting model corrects the issues of kriging, as we now:
reproduce the global feature PDF / CDF
reproduce the global variogram
while providing a model of uncertainty through multiple realizations
Cosimulation#
There is more than one method to simulate feature together. Each cosimulation method will have a ‘conditioning’ priority:
Collocated Cokriging prioritizes the histogram and variogram and may honor the correlation coefficient between the two variables
Cloud transform will honor the specific form of the bivariate relationship (cloud) between the two features but may not honor the histogram nor the variogram.
These methods start with a completed realization of the secondary feature.
primary feature is the feature being simulated, secondary feature is the previously simulated feature that is supporting the current simulation.
for example, porosity is the secondary feature and permeability is the primary feature if we cosimulate a permeability realization constrained by a previously simulated realization of porosity
Note, multiple information sources may be contradictory, in this cases lower priority information is preferentially sacrificed.
for example, the permeability variogram has a large relative nugget effect, but the porosity realization has no nugget effect and long range spatial continuity, but the correlation between permeability and porosity is very high.
Collocated Cokriging#
Collocated Cokriging makes two simplifications of full cokriging:
Markov Screening - only one (the collocated) secondary variable is considered
Bayesian Updating - cross covariance \(𝐶_{𝑧,𝑦}( \bf{𝐡} )\) is updated from the prior \(𝐶_𝑧 (𝐡)\) with the likelihood \(𝐶_{𝑧,𝑦}(0) = \rho_{z,y}\)
In this workflow we simulate porosity and log transform of permeability with:
Independent Sequential Gaussian Simulation of Two Features - each feature simulated seperately one at a time Sequential Gaussian Simulation with Collocated Cokriging - simulate a porosity realization and then cosimulate the log transform of permeability given the porosity realization.
Then we check the relationship between the porosity and log transformed permeability simulated realizations for both cases.
Load the required libraries#
The following code loads the required libraries.
import geostatspy.GSLIB as GSLIB # GSLIB utilies, visualization and wrapper
import geostatspy.geostats as geostats # GSLIB methods convert to Python
import geostatspy
print('GeostatsPy version: ' + str(geostatspy.__version__))
GeostatsPy version: 0.0.71
We will also need some standard packages. These should have been installed with Anaconda 3.
import os # set working directory, run executables
from tqdm import tqdm # supress the status bar
from functools import partialmethod
tqdm.__init__ = partialmethod(tqdm.__init__, disable=True)
ignore_warnings = True # ignore warnings?
import numpy as np # ndarrys for gridded data
import pandas as pd # DataFrames for tabular data
import matplotlib.pyplot as plt # for plotting
from matplotlib.ticker import (MultipleLocator, AutoMinorLocator) # control of axes ticks
from matplotlib import gridspec # custom subplots
plt.rc('axes', axisbelow=True) # plot all grids below the plot elements
if ignore_warnings == True:
import warnings
warnings.filterwarnings('ignore')
from IPython.utils import io # mute output from simulation
cmap = plt.cm.inferno # color map
If you get a package import error, you may have to first install some of these packages. This can usually be accomplished by opening up a command window on Windows and then typing ‘python -m pip install [package-name]’. More assistance is available with the respective package docs.
Declare Functions#
Here’s a convenience function for plotting major and minor axes.
def add_grid():
plt.gca().grid(True, which='major',linewidth = 1.0); plt.gca().grid(True, which='minor',linewidth = 0.2) # add y grids
plt.gca().tick_params(which='major',length=7); plt.gca().tick_params(which='minor', length=4)
plt.gca().xaxis.set_minor_locator(AutoMinorLocator()); plt.gca().yaxis.set_minor_locator(AutoMinorLocator()) # turn on minor ticks
Set the working directory#
I always like to do this so I don’t lose files and to simplify subsequent read and writes (avoid including the full address each time).
#os.chdir("c:/PGE383") # set the working directory
Loading Tabular Data#
Here’s the command to load our comma delimited data file in to a Pandas’ DataFrame object. We will also extract a limited sample to reduce data density. This way we can observe more of the heterogeneity from the simulation with the spatial continuity model, rather than mostly data driven heterogeneity.
df = pd.read_csv(r"https://raw.githubusercontent.com/GeostatsGuy/GeoDataSets/master/sample_data_MV_biased.csv") # from Dr. Pyrcz's GitHub repo
df = df.sample(50) # extract 50 samples
df['logPerm'] = np.log(df['Perm'].values) # calculate the log of permeability for visualization only
df = df.reset_index() # reset the record index
df = df[['X','Y','Porosity','Perm','logPerm']]
df['nPorosity'] = geostats.nscore(df=df,vcol='Porosity')[0] # Gaussian transform the features to calculate correlation
df['nPerm'] = geostats.nscore(df=df,vcol='Perm')[0]
df.head()
| X | Y | Porosity | Perm | logPerm | nPorosity | nPerm | |
|---|---|---|---|---|---|---|---|
| 0 | 990.0 | 519.0 | 0.122079 | 8.092313 | 2.090915 | -0.227545 | -0.331853 |
| 1 | 250.0 | 789.0 | 0.173883 | 559.375900 | 6.326822 | 1.644854 | 1.880794 |
| 2 | 900.0 | 300.0 | 0.135045 | 10.039742 | 2.306551 | -0.075270 | -0.125661 |
| 3 | 300.0 | 539.0 | 0.148719 | 86.109630 | 4.455621 | 0.612813 | 0.738847 |
| 4 | 230.0 | 639.0 | 0.171823 | 296.698399 | 5.692716 | 1.475791 | 1.226528 |
Let’s check the summary statistics to set the plotting minimum and maximum values.
df.describe().transpose() # summary statistics
| count | mean | std | min | 25% | 50% | 75% | max | |
|---|---|---|---|---|---|---|---|---|
| X | 50.0 | 450.400000 | 282.445299 | 40.000000 | 202.500000 | 3.850000e+02 | 700.000000 | 990.000000 |
| Y | 50.0 | 472.680000 | 257.507554 | 9.000000 | 236.500000 | 4.945000e+02 | 656.500000 | 929.000000 |
| Porosity | 50.0 | 0.132479 | 0.030776 | 0.062169 | 0.110337 | 1.374421e-01 | 0.151842 | 0.210258 |
| Perm | 50.0 | 82.769701 | 148.602047 | 0.408779 | 3.546077 | 1.083597e+01 | 75.632267 | 591.342615 |
| logPerm | 50.0 | 2.791537 | 1.950472 | -0.894580 | 1.265566 | 2.382805e+00 | 4.325618 | 6.382396 |
| nPorosity | 50.0 | -0.002897 | 1.004480 | -2.471190 | -0.659071 | 5.551115e-16 | 0.659071 | 2.326348 |
| nPerm | 50.0 | 0.005010 | 0.986040 | -2.075844 | -0.659071 | 5.551115e-16 | 0.659071 | 2.326348 |
Now we can set these values for plotting:
xmin = 0.0; xmax = 1000.0 # spatial limits
ymin = 0.0; ymax = 1000.0
nx = 100; xmn = 5.0; xsiz = 10.0 # grid specification
ny = 100; ymn = 5.0; ysiz = 10.0
pormin = 0.0; pormax = 0.22
pormean = np.average(df['Porosity'].values) # assume representative mean
permmin = 0.0; permmax = 700.0;
logpermmin = -3.0; logpermmax = 8.0;
nsmin = -3.0; nsmax = 3.0 # limits in Gaussian space
#logpermmean = np.average(df['logPerm'].values) # assume representative mean
npor_vrange = 300; nperm_vrange = 300
npor_vario = GSLIB.make_variogram(nug=0.0,nst=1,it1=1,cc1=1.0,azi1=90.0,hmaj1=npor_vrange,hmin1=npor_vrange) # assumed variograms
nperm_vario = GSLIB.make_variogram(nug=0.0,nst=1,it1=1,cc1=1.0,azi1=90.0,hmaj1=nperm_vrange,hmin1=nperm_vrange)
nxdis = 1; nydis = 1; seed = 73073; ndmin = 0; ndmax = 10 # simulation parameters
tmin = -9999.9; tmax = 9999.9 # triming limits
Let’s look at the data before we simulate. Note, we visualize permeability with a natural log transform to improve interpretation, but all of our workflow steps are conducted in the regular feature space.
plt.subplot(221) # plot porosity data
GSLIB.locmap_st(df,'X','Y','Porosity',xmin,xmax,ymin,ymax,pormin,pormax,'Location Map - Porosity','X(m)','Y(m)',
'Porosity (fraction)',cmap); add_grid()
plt.subplot(222) # plot log permeability data
GSLIB.locmap_st(df,'X','Y','logPerm',xmin,xmax,ymin,ymax,logpermmin,logpermmax,'Location Map - Log(Permeability)',
'X(m)','Y(m)','Log Permeability (log(mD))',cmap); add_grid()
plt.subplot(223) # cross plot log permeability and porosity
plt.scatter(df['Porosity'].values,df['Perm'].values,color='black',alpha=0.5)
plt.xlabel('Porosity (fraction)'); plt.ylabel('Permeability (mD)');plt.title('Permeability vs. Porosity')
plt.xlim([pormin,pormax]); plt.ylim([permmin,permmax]); add_grid()
plt.subplot(224) # cross plot log permeability and porosity
plt.scatter(df['nPorosity'].values,df['nPerm'].values,color='black',alpha=0.5)
plt.xlabel('Porosity (NSCORE)'); plt.ylabel('Permeability (NSCORE)');plt.title('NSCORE Permeability vs. Porosity')
corr = np.corrcoef(df['nPorosity'].values,df['nPerm'].values)[0,1]
plt.annotate(r'$\rho_{N[\phi],N[k]}$ = ' + str(np.round(corr,2)), (0.3,-1.35),size=12)
plt.xlim([nsmin,nsmax]); plt.ylim([nsmin,nsmax]); add_grid()
plt.subplots_adjust(left=0.0, bottom=0.0, right=2.0, top=2.1, wspace=0.2, hspace=0.2); plt.show()
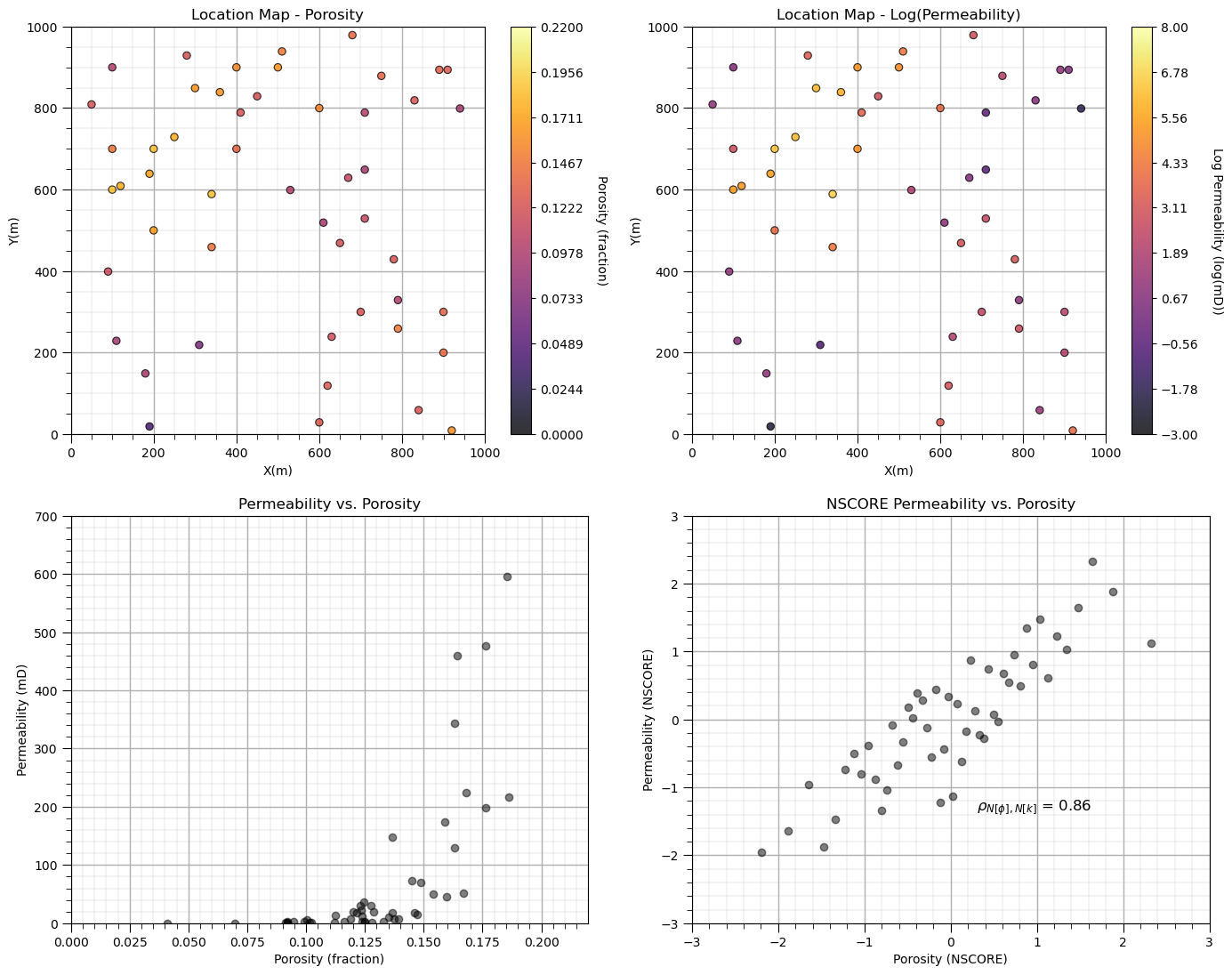
Note we have already demonstrated univariate simulation checks for:
data reproduction at data locations
histogram reproduction
variogram reproduction
in these workflows:
So for brevity, won’t repeat these checks here. Also we will just assume reasonable variogram models for demonstration; therefore, no variogram calculation and modeling.
let’s focus on reproduction of the relationship between porosity and permeability
Independent Sequential Gaussian Simulation of Two Features#
Let’s jump right to building two independent simulations and visualizing the results.
independently simulate porosity and permability
check the porosity an permeability relationship, the scatter plot.
%%capture --no-display
sim_por = geostats.sgsim(df,'X','Y','Porosity',wcol=-1,scol=-1,tmin=tmin,tmax=tmax,itrans=1,ismooth=0,dftrans=0,tcol=0,
twtcol=0,zmin=pormin,zmax=pormax,ltail=1,ltpar=0.0,utail=1,utpar=0.3,nsim=1,
nx=nx,xmn=xmn,xsiz=xsiz,ny=ny,ymn=ymn,ysiz=ysiz,seed=seed,
ndmin=ndmin,ndmax=ndmax,nodmax=10,mults=0,nmult=2,noct=-1,ktype=0,colocorr=0.0,
sec_map=0,vario=npor_vario)[0]
sim_perm = geostats.sgsim(df,'X','Y','Perm',wcol=-1,scol=-1,tmin=tmin,tmax=tmax,itrans=1,ismooth=0,dftrans=0,tcol=0,
twtcol=0,zmin=permmin,zmax=permmax,ltail=1,ltpar=0.0,utail=1,utpar=0.3,nsim=1,
nx=nx,xmn=xmn,xsiz=xsiz,ny=ny,ymn=ymn,ysiz=ysiz,seed=seed+1,
ndmin=ndmin,ndmax=ndmax,nodmax=10,mults=0,nmult=2,noct=-1,ktype=0,colocorr=0.0,
sec_map=0,vario=nperm_vario)[0]
Visualize porosity and permeability realizations and the porosity vs. permeability relationship for independently simulation realizations.
plt.subplot(221) # plot the results
GSLIB.locpix_st(sim_por,xmin,xmax,ymin,ymax,xsiz,pormin,pormax,df,'X','Y','Porosity','Independent Simulation - Porosity','X(m)','Y(m)','Porosity',cmap)
plt.subplot(222)
GSLIB.locpix_st(np.log(sim_perm),xmin,xmax,ymin,ymax,xsiz,logpermmin,logpermmax,df,'X','Y','logPerm','Independent Simulation - Permeability','X(m)','Y(m)','Log(Perm)',cmap)
plt.subplot(223)
plt.scatter(sim_por.flatten(),sim_perm.flatten(),color='red',edgecolor='white',alpha=0.2,zorder=1)
plt.scatter(df['Porosity'].values,df['Perm'].values,color='black',alpha=1.0,zorder=100)
plt.xlabel('Porosity (fraction)'); plt.ylabel('Permeability (mD)');plt.title('Permeability vs. Porosity')
plt.xlim([pormin,pormax]); plt.ylim([permmin,permmax])
sim_npor = geostats.nscore(df=pd.DataFrame(sim_por.flatten(),columns=['sim_perm']),vcol='sim_perm')[0]
sim_nperm = geostats.nscore(df=pd.DataFrame(sim_perm.flatten(),columns=['sim_perm']),vcol='sim_perm')[0]
plt.subplot(224)
plt.scatter(sim_npor,sim_nperm,color='red',edgecolor='white',alpha=0.2,zorder=1)
plt.scatter(df['nPorosity'].values,df['nPerm'].values,color='black',alpha=1.0,zorder=100)
plt.xlabel('Porosity (NSCORE)'); plt.ylabel('Log Permeability (NSCORE)');plt.title('N[Permeability] vs. N[Porosity]')
plt.xlim([nsmin,nsmax]); plt.ylim([nsmin,nsmax])
plt.subplots_adjust(left=0.0, bottom=0.0, right=2.0, top=2.1, wspace=0.2, hspace=0.2); plt.show()
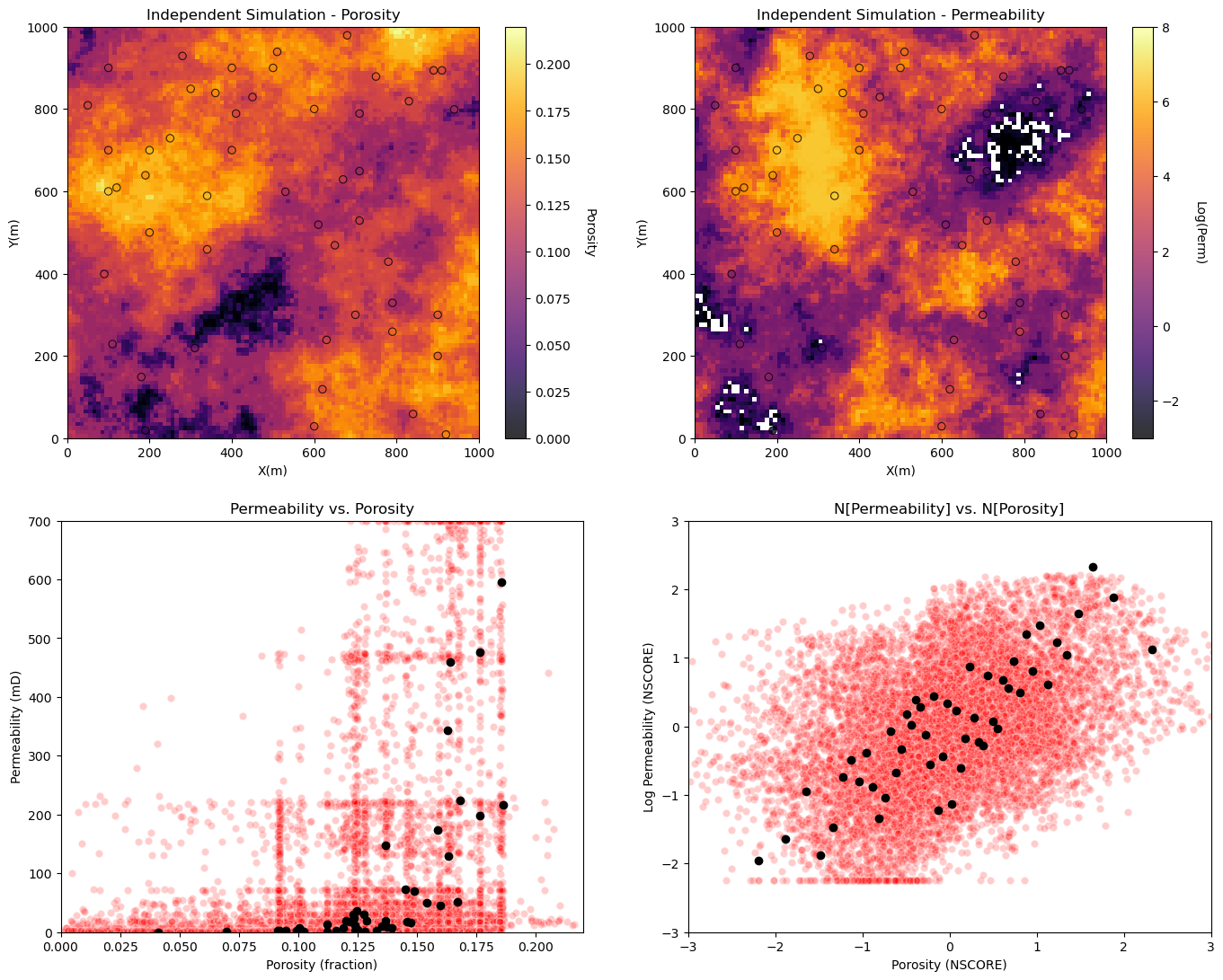
Sequential Gaussian Simulation with Collocated Cokriging#
Now let’s demonstrate collocated cokriging.
calculate a realization of porosity - DONE - we will use the porosity realization from above!
collocated cokriging realization of permeability constrained to the porosity realization
%%capture --no-display
cosim_perm = geostats.sgsim(df,'X','Y','Perm',wcol=-1,scol=-1,tmin=tmin,tmax=tmax,itrans=1,ismooth=0,dftrans=0,tcol=0,
twtcol=0,zmin=0.0,zmax=1000.0,ltail=1,ltpar=0.0,utail=1,utpar=1000.0,nsim=1,
nx=nx,xmn=xmn,xsiz=xsiz,ny=ny,ymn=ymn,ysiz=ysiz,seed=73075,
ndmin=ndmin,ndmax=ndmax,nodmax=10,mults=0,nmult=2,noct=-1,
ktype=4,colocorr=corr,sec_map=sim_por,vario=nperm_vario)[0]
Visualize porosity and permeability realizations and the porosity vs. permeability relationship for independently simulation realizations.
plt.subplot(221) # plot the results
GSLIB.locpix_st(sim_por,xmin,xmax,ymin,ymax,xsiz,pormin,pormax,df,'X','Y','Porosity','Independent Simulation - Porosity','X(m)','Y(m)','Porosity',cmap)
plt.subplot(222)
GSLIB.locpix_st(np.log(cosim_perm),xmin,xmax,ymin,ymax,xsiz,logpermmin,logpermmax,df,'X','Y','logPerm','Cosimulation - Permeability','X(m)','Y(m)','Log(Perm)',cmap)
plt.subplot(223)
plt.scatter(sim_por.flatten(),cosim_perm.flatten(),color='red',edgecolor='white',alpha=0.2,zorder=1)
plt.scatter(df['Porosity'].values,df['Perm'].values,color='black',alpha=1.0,zorder=100)
plt.xlabel('Porosity (fraction)'); plt.ylabel('Permeability (mD)');plt.title('Cosimulation Permeability vs. Porosity')
plt.xlim([pormin,pormax]); plt.ylim([permmin,permmax])
sim_npor = geostats.nscore(df=pd.DataFrame(sim_por.flatten(),columns=['sim_perm']),vcol='sim_perm')[0]
cosim_nperm = geostats.nscore(df=pd.DataFrame(cosim_perm.flatten(),columns=['sim_perm']),vcol='sim_perm')[0]
plt.subplot(224)
plt.scatter(sim_npor,cosim_nperm,color='red',edgecolor='white',alpha=0.2,zorder=1)
plt.scatter(df['nPorosity'].values,df['nPerm'].values,color='black',alpha=1.0,zorder=100)
plt.xlabel('Porosity (NSCORE)'); plt.ylabel('Permeability (NSCORE)');plt.title('Cosimulation N[Permeability] vs. N[Porosity]')
plt.xlim([nsmin,nsmax]); plt.ylim([nsmin,nsmax])
plt.subplots_adjust(left=0.0, bottom=0.0, right=2.0, top=2.1, wspace=0.2, hspace=0.2); plt.show()
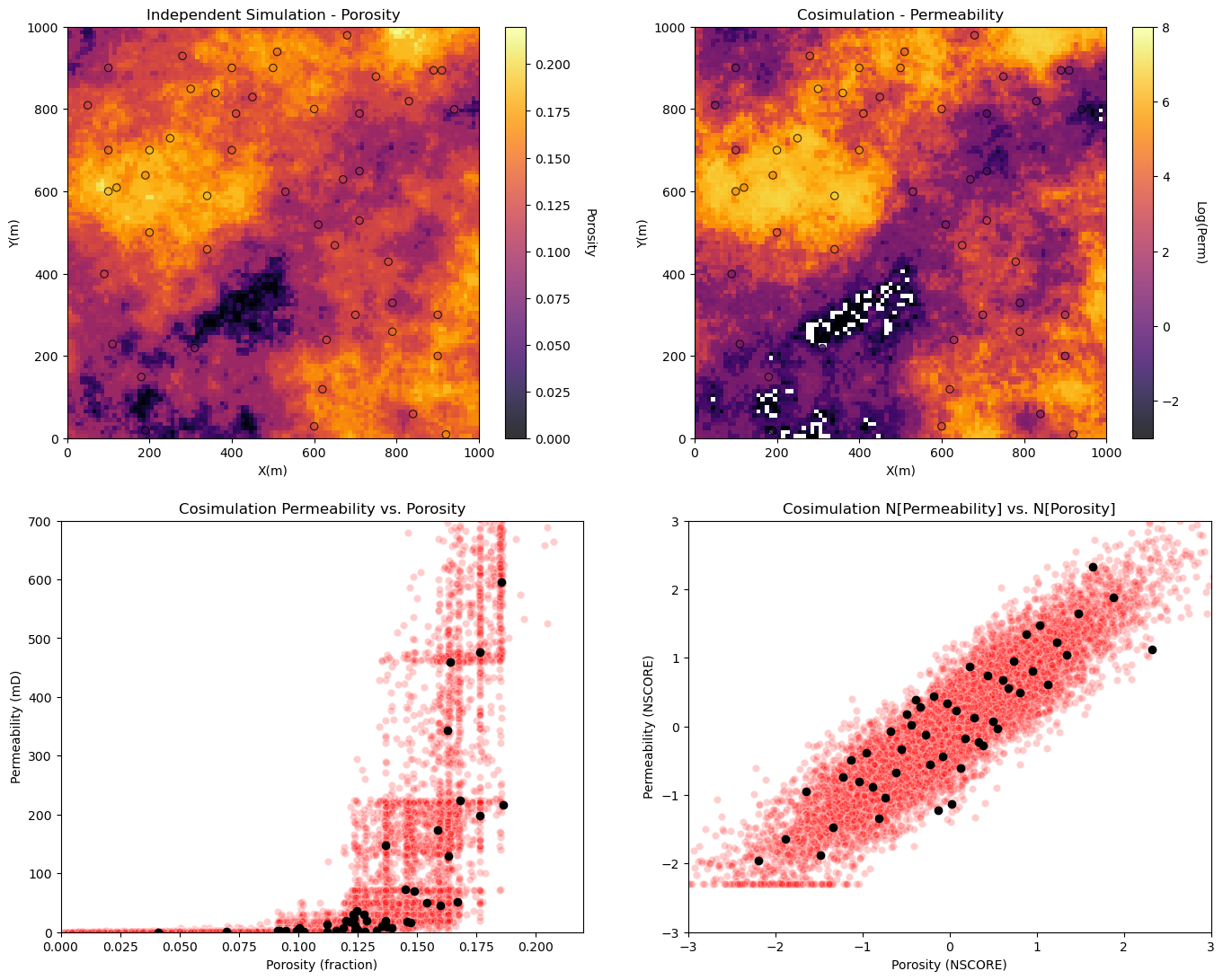
Compare the Secondary to Primary Relationship#
Let’s put all the cross plots together.
data imposes correlation - at data and within the variogram range from data, the data correlation is imposed to some degree. This is why we don’t see independence between the features with independent simulation.
unrealistic combinations - of features occur with out cosimulation!
plt.subplot(221)
plt.scatter(sim_por.flatten(),sim_perm.flatten(),color='red',edgecolor='white',alpha=0.2,zorder=1)
plt.scatter(df['Porosity'].values,df['Perm'].values,color='black',alpha=1.0,zorder=100)
plt.xlabel('Porosity (fraction)'); plt.ylabel('Permeability (mD)');plt.title('Independent Simulation Permeability vs. Porosity')
plt.xlim([pormin,pormax]); plt.ylim([permmin,permmax])
plt.subplot(222)
plt.scatter(sim_npor,sim_nperm,color='red',edgecolor='white',alpha=0.2,zorder=1)
plt.scatter(df['nPorosity'].values,df['nPerm'].values,color='black',alpha=1.0,zorder=100)
plt.xlabel('Porosity (NSCORE)'); plt.ylabel('Log Permeability (NSCORE)');plt.title('Independent Simulation N[Permeability] vs. N[Porosity]')
plt.xlim([nsmin,nsmax]); plt.ylim([nsmin,nsmax])
plt.subplot(223)
plt.scatter(sim_por.flatten(),cosim_perm.flatten(),color='red',edgecolor='white',alpha=0.2,zorder=1)
plt.scatter(df['Porosity'].values,df['Perm'].values,color='black',alpha=1.0,zorder=100)
plt.xlabel('Porosity (fraction)'); plt.ylabel('Permeability (mD)');plt.title('Cosimulation Permeability vs. Porosity')
plt.xlim([pormin,pormax]); plt.ylim([permmin,permmax])
plt.subplot(224)
plt.scatter(sim_npor,cosim_nperm,color='red',edgecolor='white',alpha=0.2,zorder=1)
plt.scatter(df['nPorosity'].values,df['nPerm'].values,color='black',alpha=1.0,zorder=100)
plt.xlabel('Porosity (NSCORE)'); plt.ylabel('Log Permeability (NSCORE)');plt.title('Cosimulation N[Permeability] vs. N[Porosity]')
plt.xlim([nsmin,nsmax]); plt.ylim([nsmin,nsmax])
plt.subplots_adjust(left=0.0, bottom=0.0, right=2.0, top=2.1, wspace=0.2, hspace=0.2); plt.show()
Michael Pyrcz, Professor, The University of Texas at Austin#
Novel Data Analytics, Geostatistics and Machine Learning Subsurface Solutions
With over 17 years of experience in subsurface consulting, research and development, Michael has returned to academia driven by his passion for teaching and enthusiasm for enhancing engineers’ and geoscientists’ impact in subsurface resource development.
For more about Michael check out these links:
Twitter | GitHub | Website | GoogleScholar | Book | YouTube | LinkedIn#
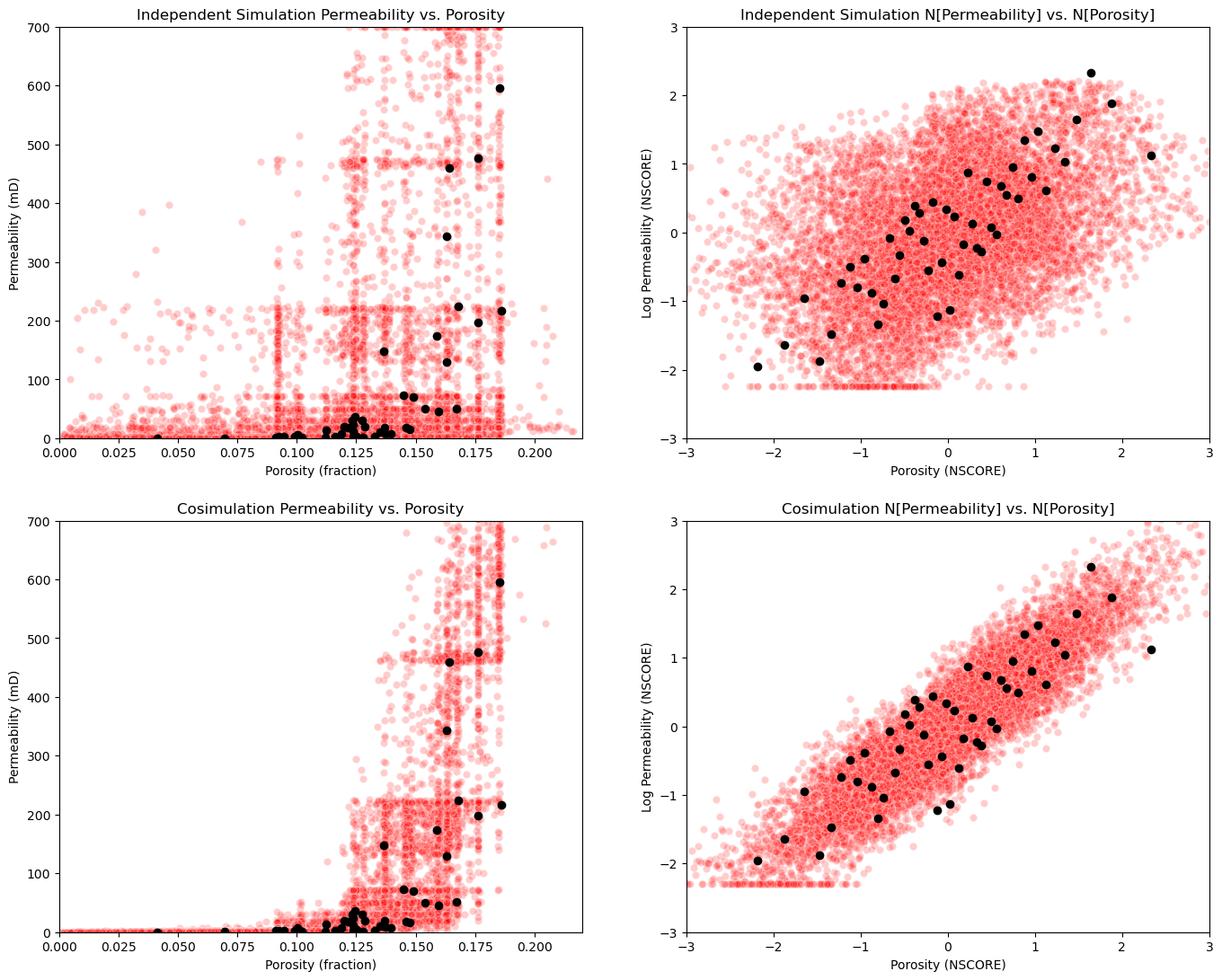
Want to Work Together?#
I hope this content is helpful to those that want to learn more about subsurface modeling, data analytics and machine learning. Students and working professionals are welcome to participate.
Want to invite me to visit your company for training, mentoring, project review, workflow design and / or consulting? I’d be happy to drop by and work with you!
Interested in partnering, supporting my graduate student research or my Subsurface Data Analytics and Machine Learning consortium (co-PIs including Profs. Foster, Torres-Verdin and van Oort)? My research combines data analytics, stochastic modeling and machine learning theory with practice to develop novel methods and workflows to add value. We are solving challenging subsurface problems!
I can be reached at mpyrcz@austin.utexas.edu.
I’m always happy to discuss,
Michael
Michael Pyrcz, Ph.D., P.Eng. Professor, Cockrell School of Engineering and The Jackson School of Geosciences, The University of Texas at Austin
Comments#
This was a basic demonstration and comparison of cosimulation vs. independent simulation with GeostatsPy. Much more can be done, I have other demonstrations for modeling workflows with GeostatsPy in the GitHub repository GeostatsPy_Demos.
I hope this is helpful,
Michael